What is poker combinatorics and how it can be applied to your game? Learn a different approach to determining your opponents' ranges.
What is Poker Combinatorics?
Combinatorics is the practice

of breaking down ranges and counting individual combinations of hands. Generally we won't have enough time during a hand to assign our opponent a specific number of combinations – it's standard practice to think more generally about our opponents range and make estimates. For example we might think something like
he has some weak top pairs and second pair type hands along with draws, but he doesn't have that many overpairs because he would have 3bet preflop. We'll refer to this as “
category-based thinking”.
This kind of thought process is sufficient in most cases, and is also pretty much all the average human brain is capable of when ranges are very wide. We'd need to be some type of savant to assign our opponent an exact number of combinations at an early stage in the hand. However as the hand progresses, ranges get significantly narrower – to the point where on the river it may be possible to assign our opponent an exact number of combos before we make our decision.
Combinatorics can also be used for off-table analysis. While it is not feasible to list the exact number of flop combos someone has during an actual hand – it should be easy enough afterwards, especially if we use
calculation software such as Flopzilla.
Why use Poker Combinatorics?
Combinatorics can be used to increase the accuracy of our standard “category-based thinking”. Previously facing a large river bet we might think along the lines of he has some busted draws and some nutted type hands. With combinatorics we can instead think he has X combos of busted draws and Y combos of nutted hands.
Even if it's an early stage in the hand where it is impractical to count exact combos, having an understanding of how combinatorics works will allow us to assign weights to our “
category-based thinking”. For example instead of thinking
he has some flush-draws, some top pairs, some underpairs, we can say
he has hardly any flush-draws, an average amount of top pair hands, and a large amount of underpairs.
Combinatorics will help us to increase accuracy of our standard "category based thinking"
With the first type of “category-based thinking”, we could easily be forgiven for assuming that these three categories of hands represent roughly an equal portion of our opponents range. In the second example, we are not quite using full combinatorics, but our knowledge of combinatorics has allowed us to add weightings to our “category-based thinking”.
Preflop Combinations
Let's start with an decent understanding of preflop distribution. This is generally an important step in being able to add weightings to
postflop ranges without needing to calculate specific combos.
There are 1326 possible combinations of starting hands. These are not distributed evenly between the different hand categories however. Some hands are simply more likely to be dealt than others.
We can divide a hole-cards grid into 3 sections.
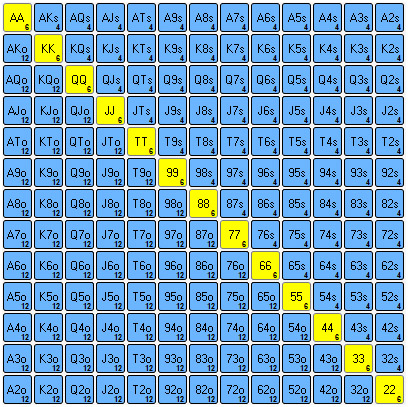
Creating a diagonal line from the top left of the grid to the bottom right of the grid are the pocket pairs. There are 6 possible combinations of every pocket pair. There are 13 different pocket pairs ranging from 22 - AA. Therefore the total number of pocket-pair combos is (13*6) = 78
Just by looking at the grid we could easily assume that there is an equal amount of hands either side of that diagonal line. It's true that there are equal amount of hand types, but there is quite a considerable difference between the number of combos. To the right of the diagonal line are the suited combos, and there are way less of these than the offsuit combos which are to the left of the diagonal line. Each type of hand has 12 offsuit combos and 4 suited combos. This means there are 3 times as many offsuit (non-pair) hands compared to suited.
In total there are 154 hand types which are not pocket-pairs. 78 of these are suited, 78 of these are offsuit.
Since there are 4 combos of every suited hand this results in (78 * 4) 312 combos.
The 12 combos of every offsuit hand result in (78 * 12) 936 combos.
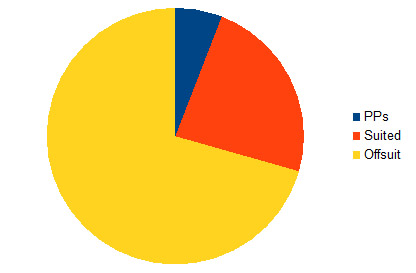
So to summarise:
Pocket-Pairs 78
Suited Combos 312
Offsuit Combos 936
----------------------------------
Total Combos 1326
Postflop Poker Combinations
Let's imagine we are now in a situation where we feel our opponent's range is narrow enough to assign a specific amount of combinations rather than estimate the weightings.
Let's look at some examples.
Example 1 - The board texture is A5272. How many combinations of A-K does our opponent have?
We know he started off with 16 combos of AK, 12 offsuit, and 4 suited. However, he can't have 16 combos of this hand any more since there is already an Ace out there. To calculate the available combinations we multiply the number of available remaining cards which make up the hand. There are 3 Aces left in the deck and 4 Kings. 3 * 4 = 12. There are 12 combos of AK.
Example 2 - The board texture is A527K. How many combinations of A-K does our opponent have?
This should be pretty simple if the last example made sense. There are 3 available Aces, and 3 available Kings. 3 * 3 = 9. 7 of these would be offsuit combos and 2 of them would be suited combos. Our opponent cannot hold AK or AK since the A and A are already on the board.
Example 3 - The board texture is K72. How many combinations of sets does our opponent have?
For
pocket pairs we need to use

a slightly different method. First count how many available cards there are to make the pocket pairs. For example, to make a set of Sevens there are 3 Sevens remaining in the deck. The formula (where X is number of available cards is) (X * (X-1)) / 2
It looks complicated but is actually very simple. There are 3 cards. We multiply it by 2 to make 6. Then we divide by 2. There are 3 combos of each set (Kings, Sevens, Twos). There are 3 possible sets meaning there are 9 combos of sets in total here
So if we wanted to know how many possible combinations of 88 there are here (no set), we know there are 4 available cards so we can calculate (4*3)/2 = 6 combos.
It looks complicated but is actually very simple. There are 3 cards. We multiply it by 2 to make 6. Then we divide by 2. There are 3 combos of each set (Kings, Sevens, Twos).
Or imagine there are 2 sevens out there and we want to know how often someone has made Quads. (2*1)/2 = 1 combo. Multiply the part in brackets first and then divide by two.
Some calculations are a little more complex. For example working out how many flush-draws opponent has. On a two-tone board we know he will have 1 combo of each suited hand that can make a flush-draw. But we obviously don't just count all possible flush-draws; we have to think about which of these are actually in his range. So in most situations we can discount holdings like
27.
Final Note on Poker Combinatorics
Keep in mind that combinatorics can not be used independent of frequency. A common mistake when first beginning to look at combinatorics is simply looking at which hands opponent might have rather than the frequency with which he continues.
For example, imagine a typical bluff-catch situation where we want to work out whether opponent has enough bluffs for us to make a profitable call. We might calculate that he has 100 combinations of possible bluffs and only 10 combinations of possible value-hands. Easy call? Not necessarily.
A common mistake when first beginning to look at combinatorics is simply looking at which hands opponent might have rather than the frequency with which he continues.
We can't just assume he is firing all of his bluffs. Some guys just never bluff – so just because they reach the river with a ton of
possible bluff combos does not automatically mean that calling down is correct. We calculate the possible bluff combos and then we assign a bluff frequency before making our decision.
 of breaking down ranges and counting individual combinations of hands. Generally we won't have enough time during a hand to assign our opponent a specific number of combinations – it's standard practice to think more generally about our opponents range and make estimates. For example we might think something like he has some weak top pairs and second pair type hands along with draws, but he doesn't have that many overpairs because he would have 3bet preflop. We'll refer to this as “category-based thinking”.
of breaking down ranges and counting individual combinations of hands. Generally we won't have enough time during a hand to assign our opponent a specific number of combinations – it's standard practice to think more generally about our opponents range and make estimates. For example we might think something like he has some weak top pairs and second pair type hands along with draws, but he doesn't have that many overpairs because he would have 3bet preflop. We'll refer to this as “category-based thinking”.

 a slightly different method. First count how many available cards there are to make the pocket pairs. For example, to make a set of Sevens there are 3 Sevens remaining in the deck. The formula (where X is number of available cards is) (X * (X-1)) / 2
a slightly different method. First count how many available cards there are to make the pocket pairs. For example, to make a set of Sevens there are 3 Sevens remaining in the deck. The formula (where X is number of available cards is) (X * (X-1)) / 2 

